Joy of Vex Day 18 ​

intrinsics

Intrinsics ​

Create a primitive sphere (as in the default sphere type, none of the poly or nurbs types). Append a transform sop, and rotate/translate/offset it so its fairly deformed, like this:

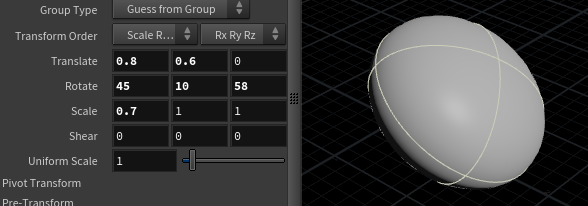
Now stop and think about this... where is that translate/rotate/scale info being stored?

'Right there Matt' you say, 'on the transform sop'.

Well yes and no. That's the modifier that caused this deformation, but we could write this geo out to disk, read it back in, and it would still look like this without the transform sop. So where is it being stored on the geo itself, in the geo spreadsheet?

Translate is obvious, that's @P. But rotation? If this were a polygon sphere then obviously it doesn't matter, as the rotation is baked into each point's @P, but this is a primitive sphere. It's acting like a big standalone particle, so there's no 'outer skin' of points to rotate.

If this were a packed primitive then rotation might be stored on @orient, but no, its not there. Neither is @scale nor @pscale.

What voodoo is going on here?

The answer is over on the primitives view of the geo spreadsheet. Switch over, click the 'intrinsics' drop down, choose 'Show All Intrinsics':

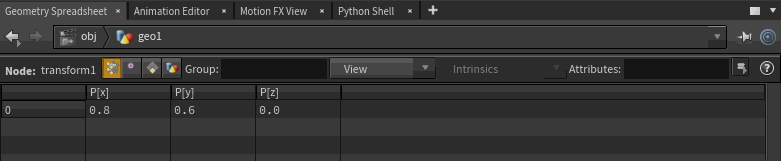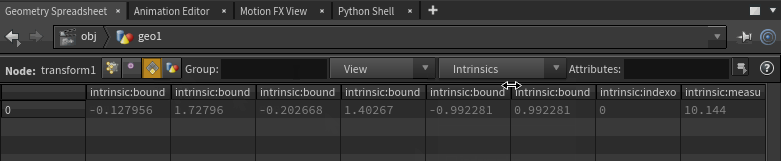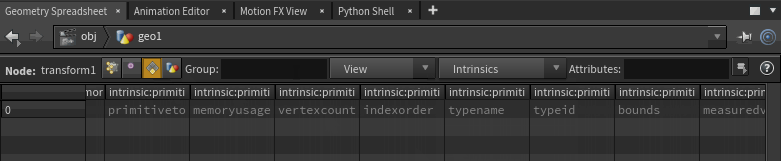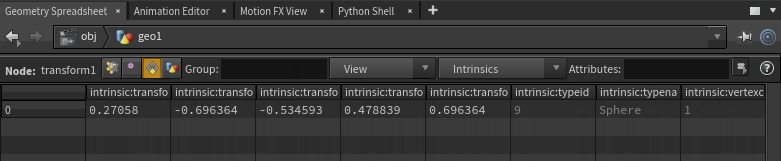
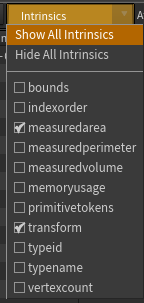
Aha! Hidden attributes! You can scroll across the entire list as shown above, or use the dropdown to view a subset:

So what's an intrinsic? Lets go find a dictionary definition:

intrinsic - being an extremely important and basic characteristic of a person or thing.

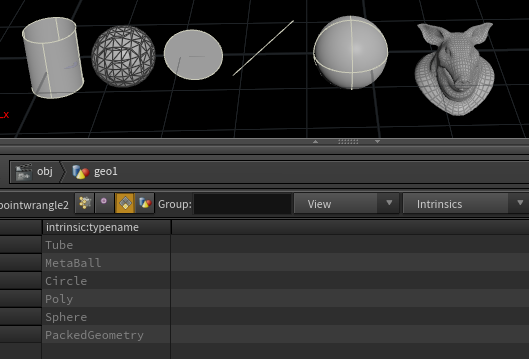
Ok, so these are important base characteristics of a primitive. For example, if you look in the intrinsics list there's one for 'typename'. Enable it, you can see that it's 'sphere' in this case. Throw a bunch of random objects together, merge them, view the typename intrinsics attribute, this is how Houdini knows what kind of geo to draw for each primitive:

Another intrinsic you'll find in there is 'transform'. View it for the sphere, you'll see its an array of numbers. Well, more than an array, its a 3x3 matrix.

As I alluded to in the previous chapter, a 3x3 matrix is a compact way to store the rotation and scale of an object. I used to remember why it combines rotation and scale, but I've forgotten, and its not important in the context of this tutorial (I'll find some links on matricies later if you're interested). Anyway, you can think of a default matrix (called an identity matrix) as a fresh transform sop; it has scale at 1 1 1, and applies no rotation. The 3x3 set of numbers that represents this 'do nothing' state has a recognisable form, (similar to the 'no rotation' form of @orient):

1 0 0
0 1 0
0 0 1

You can create an identity matrix manually with those numbers:

 matrix3 m = {1,0,0,0,1,0,0,0,1};

 matrix3 m = {1,0,0,0,1,0,0,0,1};

but an easier shortcut is to use the vex ident function:

 matrix3 m = ident();

 matrix3 m = ident();

Now, notice that if you view all the intrinsics in the geo spreadsheet, most are dark gray? This means they're read only. The 'transform' intrinsic however is in a lighter colour, this is a visual clue that you can write to this intrinsic.

So, lets make a leap of logic. Our sphere has been rotated and scaled. There's no other place for that rotation and scale to be stored except for this transform intrinsic. That intrinsic can be written to. So if we write an identity matrix to that transform, will that remove the rotation and scale?

One more thing to know before trying; you don't use the @attrib syntax for intrinsics, you need a function, setprimintrinsic. Similar to using the point() function, you need to specify the geo input to use, the intrinsic name, the primid to write to, and the value to insert.

 matrix3 m = ident();
 setprimintrinsic(0, 'transform', 0, m);

 matrix3 m = ident();
 setprimintrinsic(0, 'transform', 0, m);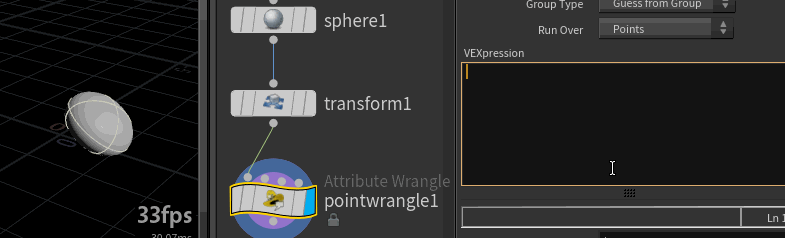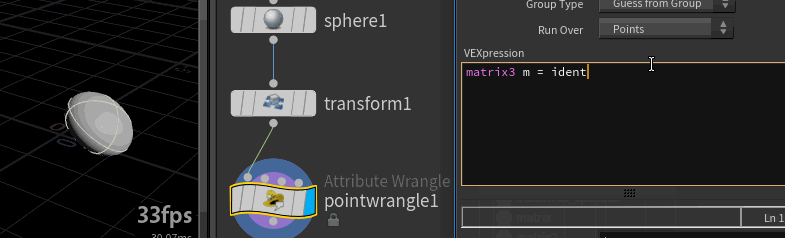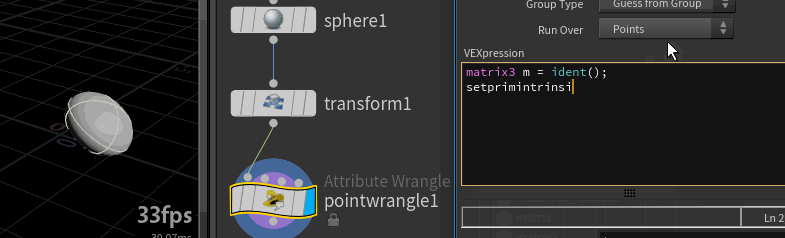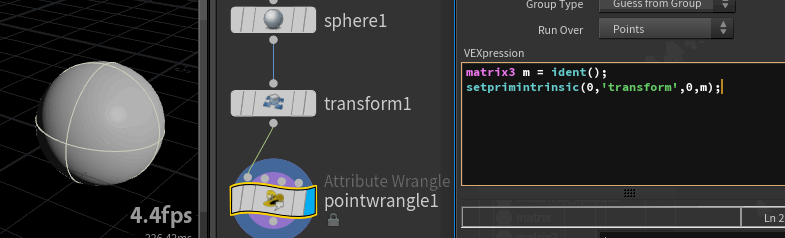

Great success!

Intrinsics vs orient and scale ​

What happens then if we apply @scale and @orient to this sphere?

I'll tell you; nothing. @orient and @scale only have an effect when fed to a copy sop (or other things that are instance attribute aware like packed rbd sims or the instance object node). But there'll probably be situations where you have @scale/@orient, and you want it to drive the primitive. In these cases, you have to update the transform instrinsic yourself. This means creating a matrix3, scale, it, orient it, apply it:

 @orient = quaternion({0,1,0}*@Time);
 v@scale = {1,0.5,1.5};

 matrix3 m = ident();
 scale(m, @scale);
 m *= qconvert(@orient);

 setprimintrinsic(0,'transform',@ptnum,m);

 @orient = quaternion({0,1,0}*@Time);
 v@scale = {1,0.5,1.5};

 matrix3 m = ident();
 scale(m, @scale);
 m *= qconvert(@orient);

 setprimintrinsic(0,'transform',@ptnum,m);

There's some new things going on there; to scale a matrix you use the scale function, where specify the matrix to scale, and the vector to scale it by. This is one of a handful of functions where it does it 'in place', ie, you don't assign it to a variable like you would normally, so this will error:

 m = scale(m, @scale);

 m = scale(m, @scale);

You just call the function, and it will be applied directly to the matrix you specify. Why? Well, for the most part this is used if a function will return multiple values, eg the xyzdist function we'll get to later will calculate a primitive id, a distance, and a uv. There's no way to do this sort of thing:

 primid, dist, uv = xyzdist( 0, blah, blah);

 primid, dist, uv = xyzdist( 0, blah, blah);

so instead the variables you want to return are wrapped inside the function:

 xyzdist( 0, blah, primid, dist, uv);

 xyzdist( 0, blah, primid, dist, uv);

That (sort of) makes sense there, but the vex scale function just returns a single matrix, why do this? Honestly, I don't know. There's a few corners of vex that are little weird, scale (and its cousin rotate) are in those corners.

Anyway, back to this code snippet. The next line converts orient to a matrix, then multiplies it against our matrix. Matricies can be combined by multiplying, similar to how quaternions can be combined with the qmultiply function.

Finally that matrix is assigned to the transform intrinsic.

I wager that's a lot to take in, but the main thing to keep in mind is that you can construct a matrix out of instance attributes, and apply them to the transform intrinsic as if you were using a copy sop.

Transform vs Packedfulltransform ​

The transform intrinsic is a matrix3, is read/write, and contains the rotation and scale for your primitive.

If you have packed geo, there'll be a packedfulltransform intrinsic. It's a 4x4 matrix, is read only, and it contains rotation, scale AND position.

To convert from a 4x4 to a 3x3 matrix (ie, just extract the scale and rotation values), you cast in the same way we've done int to float casting way back in the early days of these tutorials:

 matrix3 m = matrix3( myfancy4x4matrix);

 matrix3 m = matrix3( myfancy4x4matrix);

Oh you want the full version? Ok then. First, lets get the packedfulltransform, and store it as a matrix4 temp variable called pft:

 matrix pft = primintrinsic(0,'packedfulltransform',@ptnum);

 matrix pft = primintrinsic(0,'packedfulltransform',@ptnum);

When debugging this sort of stuff, it can be handy to stuff a matrix into a geometry attribute to make sure it's working as you expect. To do that you prefix the @ symbol with '4', meaning a 4x4 matrix:

 4@a = pft;

 4@a = pft;

If you inspect the values in the geo spreadsheet, you'll see that the position of the packed geo is put into the last 4 values of the matrix (well, the last row, the final value isn't used). If you were to look at this as a written-on-paper matrix, you'd get this kind of thing:

Interpreting matricies is well beyond the scope of this tutorial, but the important thing to know is that there's 2 regions to this matrix:

The green region represents the rotation and scale, the red numbers represent translation. When you convert from a 4x4 to a 3x3 matrix, all it does is keep the green bit and discard the rest. You can just assign directly and you'll get a warning, but if you want to be neat and tidy, you cast it:

 matrix3 rotandscale = matrix3(pft);

 matrix3 rotandscale = matrix3(pft);

or again, if you want to debug or inspect this as a geometry attribute:

 3@b = rotandscale;

 3@b = rotandscale;

Why tell me all this ​

I assume by now you're wondering what the point of all this is. Well, if you start getting fancy with bullet, packed prims, copy sops etc, you'll find yourself occasionally in places where you want to transfer the animation from a sim to something else, or from alembic archives to points, or some other curious edge case. In these cases, you often have to go and fetch intrinsic transforms from one place, and apply them to another.

Further, while I've written up some tips on how to do this on the HoudiniDops page, I've been warned that those tricks aren't guaranteed to work. Alembic archives in different formats do different things (and might even have yet another intrinsic, 'abcfulltransform' or similar), packed fragments vs packed disk prims can behave slightly differently.

The point is that intrinsics can be useful to get you out of a tight spot, useful to know where they are and how to get at them.

This seems messier than expected ​

Yes. It would be good to have this all be unified and clean right? Better tell sidefx, make your voice heard. 😃

Transform by attribute ​

A recent addition to Houdini is the transform by attribute sop. For the most part it saves you the effort of going to vex and using the setprimintrinsic stuff, and knows how to apply the right attribute to the right geometry in the right way. It can sometimes get snagged on edge cases, in which case you can be smug that you know some of the vex methods to do what you need.

Other intrinsics ​

There's a few that can be handy, assuming they have meaningful data. Its often worth a browse through all the intrinsic types, see if theres stuff you can steal. Things like area, perimeter, bounds, closed (that tells you if a prim is a polygon prim or a polyline outline), all can be handy. Its also interesting to see which ones can be written to. Eg, I just noticed that the closed intrinsic is read/write, so can do this sort of thing to randomly convert polys to polyline outlines. Completely useless of course, but one day, who knows?

 int openclose = int(rand(@primnum+@Frame)*2);
 setprimintrinsic(0,'closed', @primnum, openclose);

 int openclose = int(rand(@primnum+@Frame)*2);
 setprimintrinsic(0,'closed', @primnum, openclose);

Note that intrinsics often aren't designed to be manipulated this way. A way to think about it is 'well, if it were an openly modifiable attribute, it would probably be exposed as a normal attribute rather than as a semi-hidden intrinsic'.

Still, you're on day 18 of this course, I think you're up to it. Try it, if it crashes Houdini, then you know you probably shouldn't do that.

Exercises ​

1. What other intrinsics can you find? Check what is available on some more exotic geometry types like volumes vs vdbs, packed alembics
2. We've gone through most of the common attribute types and how to define them by prefixes, search the help to find the full list
3. What other intrinsics are writable?
4. Are there any intrinsics at other geometry levels? (Ie point intrinsics, vertex intrinsics, detail intrinsics)

prev: JoyOfVex17 this: JoyOfVex18 next: JoyOfVex19
main menu: JoyOfVex