Appearance
Joy of Vex Day 19
primuv, xyzdist
Primuv
How do you stick things to geometry in vex? We learned about minpos earlier, but thats not really sticking as much as finding the closest position.
To properly stick stuff you use primuv. Give it a primid and a uv coordinate, it will return the attribute you specify at that uv location.
vex
vector uv = chv('uv');
@P = primuv(1,'P',0,uv);
@N = primuv(1,'N',0,uv); vector uv = chv('uv');
@P = primuv(1,'P',0,uv);
@N = primuv(1,'N',0,uv);Feed a single point to the input0, a 1 poly grid to input1, then that to a copy sop, you can stick an object to the grid at the uv coordinate you specify:
Ok, that's pretty uninspiring. But look what happens if we animate the grid with a transform sop, P and N from primuv stay locked to the grid.

Why is the object twisting a little as the grid spins? Because we don't have @up defined, so it tries its best to point the object-x towards world-x instead.
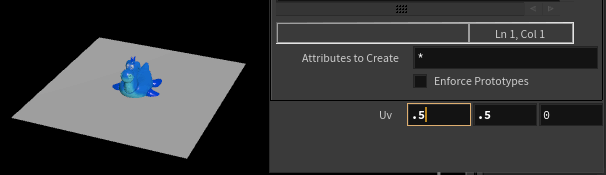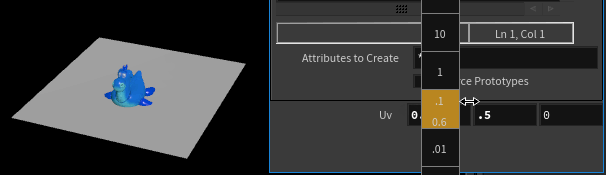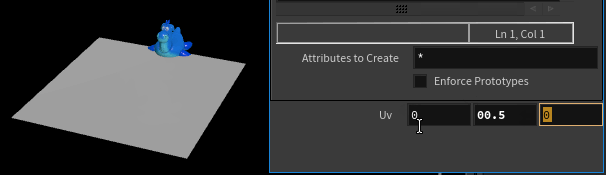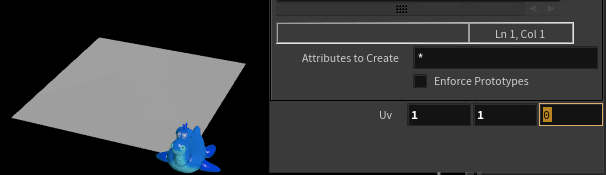
We can also animate the uv coordinate and see the object update accordingly. Eg, we can set the uvs to spin in a circle use sin and cos, which will be in a range of -1 to 1, centered on 0, which we then fit to the radius of a circle we want, then add 0.5 0.5 to push it to the center:
vex
vector uv;
uv.x = sin(@Time*10);
uv.y = cos(@Time*10);
uv = fit(uv, -1,1,-0.2,0.2);
uv += {0.5,0.5};
@P = primuv(1,'P',0,uv);
@N = primuv(1,'N',0,uv); vector uv;
uv.x = sin(@Time*10);
uv.y = cos(@Time*10);
uv = fit(uv, -1,1,-0.2,0.2);
uv += {0.5,0.5};
@P = primuv(1,'P',0,uv);
@N = primuv(1,'N',0,uv);
Or more practically, this works on a deforming nurbs mesh. Here I've switched the grid to nurbs mode, used a mountain sop to give it some animated noise, now we have the geo rolling over a stormy sea (the nurbs grid is treated as a single prim):

Note that in all these examples, whats going on is giving us an interpolated value; it knows the value of P and N at the points that define the primitive, and by us specifying a uv, its using that to interpolate between those points for the attribute you specify.
Uvs vs parametric uvs
Those with sharp eyes might have wondered how we can specify uv coordinates to the primuv function, but we have no @uv attributes. In fact, even if you do create uv's in whatever way you specify, the behaviour will be the same.
Here I've put a uv project and uv quickshade on the grid before the wrangle, and I can slide around the uv properties as much as I want, the rubber toy still moves in exactly the same way:
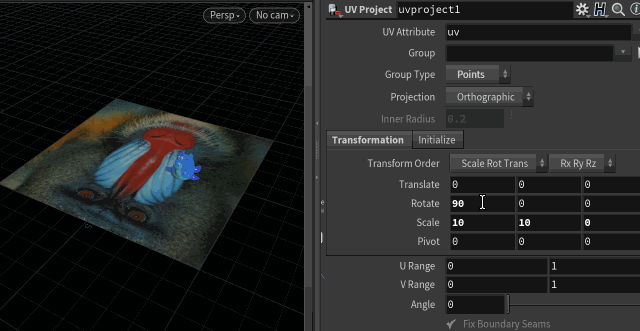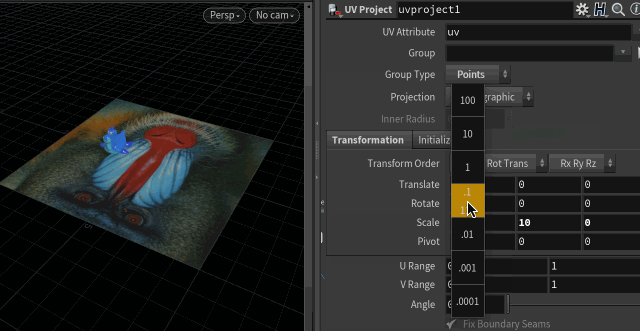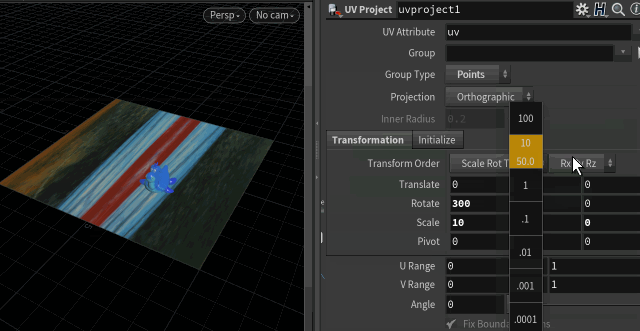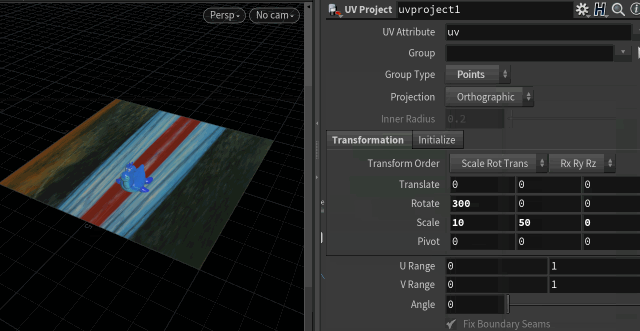
This is because primuv (and a few other tools) use what are called parametric uvs. This is calculated per primitive, and can be thought of as a 2d bounding box style calculation, on the surface of the prim. It takes the first vertex of the prim, then the last, and uses that to define a 0:1 gradient across it. You can visualise this with a scatter sop, output tab, turn on 'sourceprimuv', but change the name to 'Cd'.
Now increase the scatter count, and increase the number of divisions on the grid, you can see that the red/green gradient corresponds to each prim:

If my calculations are correct, all surface type primitives (so no volumes/metaballs) should have parametric uv's. They won't always be in a square shape as you get with a 4-sided poly, but they should guarantee that you can reference any single position on the primitive shape without overlaps. Here's a primitive tube, sphere, line, grid, circle, and their corresponding parametric uvs:

Incidentally, if you've ever done some mantra rendering, applied a texture to a default grid, and wondered why you get a per-face uv even if you haven't assigned anything, this is why; in the absence of 'real' uv's, mantra will fall back to parametric uv's instead.
xyzdist
minpos gives you the closest @P on geometry when you feed it some arbitrary position. Primuv gives you any attribute you want if you give it a parametric uv location. But what if we want to bridge these two ideas? Ie, we have a position in 3d space, and we want to get an attribute from the closest position on some geometry. This is what xyzdist does.
Similar to the rotate and scale matrix functions, because this function can return more than one piece of information, but vex doesn't support that kind of thing, you setup placeholder variables first, call the function referencing those variables, and afterwards, those variables will contain the information you need.
Makes more sense with an example. Go back to a 10x10 grid, create a point with an add sop and position it somewhere near the grid, connect the point to the first input of a wrangle, grid to the second, and try this:
vex
i@primid;
v@uv;
@dist;
@dist = xyzdist(1, @P, @primid, @uv); i@primid;
v@uv;
@dist;
@dist = xyzdist(1, @P, @primid, @uv);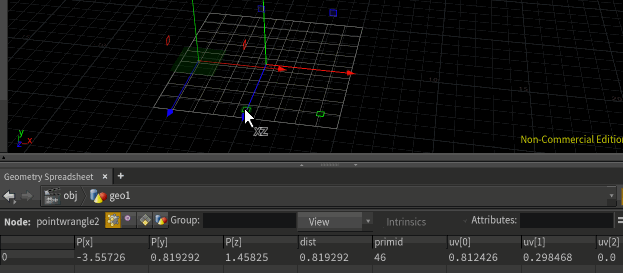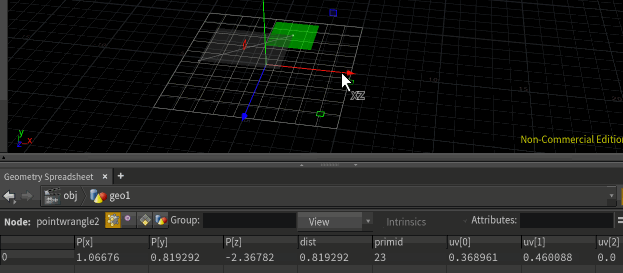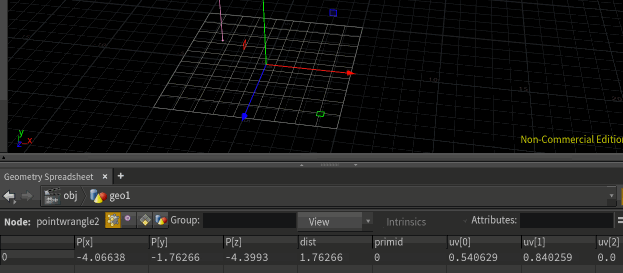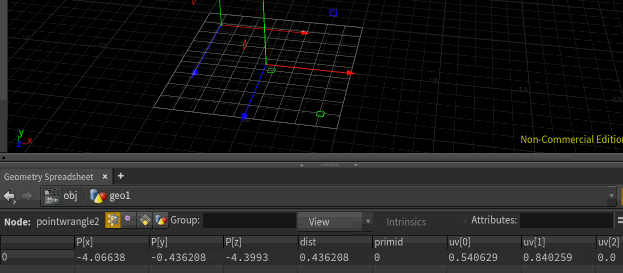
To save some typing, and so that we can easily visualise the values, I'm directly using geometry attribues rather than values.
xyzdist in its default form just returns distance to the surface, and thats the default value that gets returned, which we're saving as @dist. But it can also record the id of the closest primitive, and the parametric uv of the position on that primitive, which I'm saving here as @primid and @uv. In the geometry spreadsheet in the gif above, you can see the distance, primid and uv all updating as I move the point around.
Now that we have a primid and uv, you could use the primuv function to query information. For example, we can query @P, essentially doing what minpos() does (and its what you had to do before the minpos function arrived in H16):
vex
i@primid;
v@uv;
@dist;
@dist = xyzdist(1,@P, @primid, @uv);
@P = primuv(1,'P',@primid, @uv); i@primid;
v@uv;
@dist;
@dist = xyzdist(1,@P, @primid, @uv);
@P = primuv(1,'P',@primid, @uv);But unlike minpos, you're not limited to querying the closest position, you can query whatever you want. Eg, if you have random colours on the grid, you can sample that too. I've run this code, then copied a sphere to that point:
vex
i@primid;
v@uv;
@dist;
@dist = xyzdist(1,@P, @primid, @uv);
@P = primuv(1,'P',@primid, @uv);
@Cd = primuv(1,'Cd',@primid, @uv); i@primid;
v@uv;
@dist;
@dist = xyzdist(1,@P, @primid, @uv);
@P = primuv(1,'P',@primid, @uv);
@Cd = primuv(1,'Cd',@primid, @uv);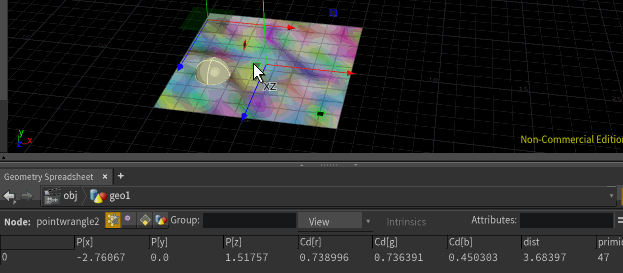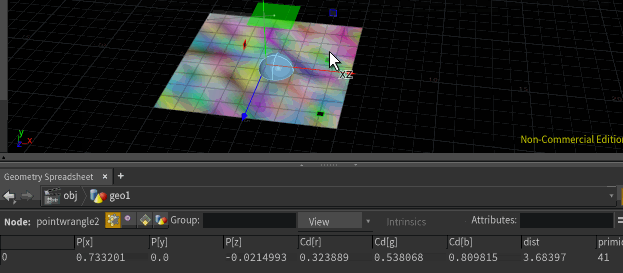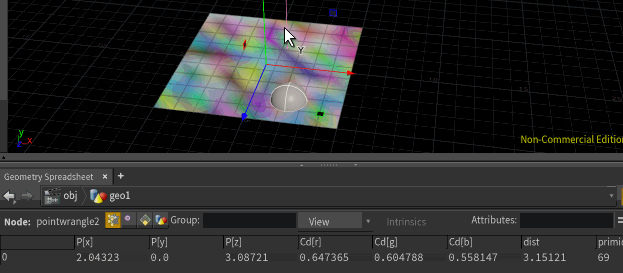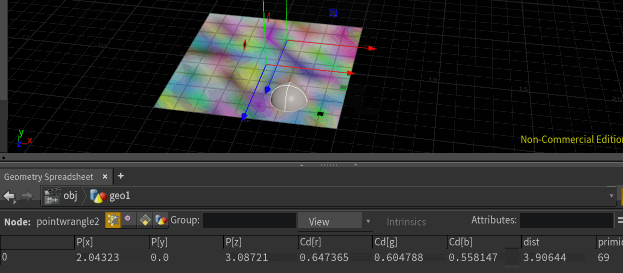
Henry Foster goes into a lot more detail on his blog:
http://www.toadstorm.com/blog/?p=465
Attribute Interpolate
It's worth pointing out that you can sometimes avoid vexing yourself into a corner and use the attribute interpolate sop instead. It's primary purpose is to make scattered points be stable on animated geometry, but if you look at how it works and the attributes it expects, it's very similar to the ideas shown so far. It assumes that you have points with i@sourceprim and and v@sourceprimuv, will use those to lookup geometry from the second input, and interpolate attributes from what it finds (mostly people just want @P).
Exercises
- Use modulo with time to animate the uv vector you feed to primuv to have shapes smoothly slide across a single poly grid
- Find the example on this site of using attrib interpolate with a scatter sop, see how similar it is to the primuv trick
- Try primuv with curves/polylines, see if you can push points along a curve, see how you might use it for a simple crowd system
- Using the above, how would you get cars to properly orient themselves on the curve? The lazy way is to use a trail sop, set it to calculate @v, and if there's no other @N/@up/@orient attribs, will point the copied geo along @v, but how would you then convert @v to @orient so its a stable rotation? There's hints elsewhere on the wiki for this, but see if you can work this out yourself.
- See if you can replicate the workflows shown above with an attribute interpolate sop (some work, some don't), and vice versa, see if you can do what an attribute interpolate does in vex.
prev: JoyOfVex18 this: JoyOfVex19 next: JoyOfVex20
main menu: JoyOfVex